Решаем задачи по геометрии

Любой студент или школьник должен запомнить одну простую истину – можно решить любую задачу, какой бы трудной она не казалась на первый взгляд. Ведь задачи составляют для закрепления теоретических знаний и отработки определенных практических навыков, следовательно, для того, чтобы их решали, а не в целях третирования учащихся.

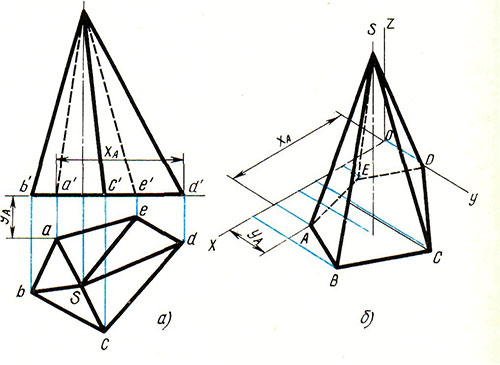
Разумеется, есть такие сверхсложные варианты задач, которые пытаются разрешить столетиями. Однако их количество не так уж и велико, да и награда за найденное решение будет больше «пятерки» за контрольную работу или экзамен. Встретить нечто подобное в школьной программе невозможно.

Следовательно, для того, что бы научиться решать задачи по геометрии необходимо иметь желание, усидчивость и тренированные мозги и воображение. Других путей освоить эту интересную область математики не существует, мы не берем в расчет решебники со 2 по 11 класс и всевозможные ГДЗ, очень сильно облегчающие жизнь студенту. Однако, получив все необходимые навыки и тщательно проштудировав теорию, можно приблизиться к пониманию того, что существует определенная методика решения задач по геометрии, способная упростить процесс решения любой задачи. Для этого необходимо всегда выполнять следующие действия:

1. Изучив условие задачи, сразу же займитесь составление чертежа. Без толковой схемы затруднительно решить даже простую задачу, а сложную – практически невозможно. При этом не жадничайте, экономить место в тетради вы будете в другом случае. Визуализация условия задачи по геометрии требует максимально возможного объема на тетрадном листе. Чем крупнее чертеж, тем нагляднее и доступнее будут решение задачи.
2. Построив чертеж или схему, нанесите на нее все известные данные – прямые и косвенные (которые можно получить путем промежуточных вычислений). Поверьте, решение задачи может «всплыть» сразу же после того, как вы сделаете эту нехитрую работу.
3. Не полагайтесь во всем на интуицию и пространственное воображение, без знания теоретической базы серьезных результатов вам не достигнуть. При этом можно не забираться в дебри формулировок, а запомнить и осмыслить несколько десятков распространенных формул и правил.
4. Помните о небольших хитростях: о задачах, которые решаются методом «первого и второго треугольника», об использовании центра окружности в соответствующих случаях (всегда соединяйте «интересные» точки вписанных и описанных фигур с центром окружности), о правилах суммы углов треугольника и прочих несложных способах вычисления промежуточных величин, которые помогут в поиске искомого значения.
5. Всегда записывайте «полет» вашей мысли. После трех-четырех связок вы можете потерять нить рассуждений и потратить значительное время на попытки вспомнить уже принятое решение. После решения задачи обязательно проверьте себя. Это поможет избежать досадных ошибок, которые могли ускользнуть от вашего внимания, увлеченного удачными поисками варианта решения задачи.

В заключение несколько слов о неудачах и патовых ситуациях, когда все потуги учащегося не приводят к положительным результатам. Для выхода из тупика используйте несколько простых действий:

Во-первых, переверните схему задачи. Посмотрите на чертеж буквально «под другим углом». Вероятно, вы что-то упустили или не заметили, и решение может прийти само собой.

Во-вторых, отложите «затруднительную» задачу в сторону, отвлекитесь на другое дело. Через десять минут мозг «перезагрузится», «накатанная» схема, которая привела вас в тупик, забудется и можно начинать искать новый путь к решению задачи.

В-третьих, примените тактическую хитрость. Вспомните, что вы проходите по программе на данный момент. На контрольной работе вам, как правило, будут задавать задачи с четкой привязкой к изученной теории. Постарайтесь заново оценить условие с точки зрения именно «последних» теоретических материалов. Например, если вы занимались изучением хорды или биссектрисы, постарайтесь «по максимуму» заполнить чертеж именно этими элементами.